Nagyon hasznos tehát ma is, ha megtanuljuk, hogyan kell egy kötvény árfolyamát, hozamát kiszámolni. Kötelezőnek persze nem kötelező hozamot számolni, ez nem kell, hogy bárkit eltántorítson a befektetéstől. Ugyanis ma már minden bank, kötvénykibocsátó vagy éppen az Államkincstár fel kell hogy tüntesse a befektetések pontos hozamát termékein. A három mutató közül – EHM, THM, EBKM – a kötvényeknél az EHM-et használják. A változó kamatozású papíroknál azonban nem találunk ilyet, mert ott még nem ismerjük a jövőbeli kifizetéseket, így bármiféle számítás csak szükségképpen pontatlan becsléseken alapulna.
Nem árt azonban, ha értjük, amit látunk, és a hozamszámítás megtanulása más befektetéseknél is hasznos lehet. Előző cikkünk számpéldája szerint a kisiskolások is tudják, hogy ha tízezer forintot egy évre tíz százalékos kamattal helyezünk el valahol, akkor 11 ezer forint lesz az eredmény. Fordítva, ha tízezer forintunkból 11 ezer lett, akkor tíz százalék volt a kamat. Ha pedig arra a kérdésre keressük a választ: mennyit kell befektetnünk ahhoz, hogy tíz százalékos hozamelképzelés mellett 11 ezer forintot kapjunk a végén, akkor is kézenfekvő a válasz.
A legegyszerűbb hozamszámítást már mindenki tudja fejben

Mindegyik egy egyszerű, fejben történő osztás vagy szorzás volt, sorrendben: 10 000x1,1, 11 000/10 000=1,1 és 11 000/1,1. (Az 1,1-ből a 0,1 a tíz százalékos kamat kifejezése, hiszen a százalék egy századrészt, a tíz százalék tíz századrészt, azaz egy tizedrészt jelent. Az 1-et mint segédszámot pedig azért kell hozzáadnunk, mert az a száz százalék, azaz a kiinduló befektetésünk, amit a futamidő végén egy az egyben visszakapunk.)
A félévek nem hajlandók egyformák lenni
A gyakorlatban a bonyolultabb esetekben is lényegében ugyanezt csináljuk. Szintén a korábbi példánál maradva, egy egy éves, tíz százalékos hozamú diszkont kincstárjegynél is ugyanezeket az osztásokat kell elvégezni, csak a 10 000 forintos ár helyett a 9090,91 forintos eladási ár, a 11 000 forintos végső lejárat helyett pedig egy 10 000 forintos lejárati kifizetés áll. Ugyanígy, ha például 10 600 forintot fizet egy lejáró kötvény, és 10 200 forintért lehet hozzájutni, akkor 10 600/10 200, azaz 3,92 százalék a hozamunk (Kerekítés után 1,0392 az osztás eredménye, amiből levonunk egyet, és megszorozzuk százzal.)
És mi a helyzet akkor, ha ezt a 3,92 százalékot nem egy évre, hanem fél évre kaptuk? Még ez is nagyon könnyű, 3,92*2=7,84 százalék lesz az éves hozamunk. De már csak körülbelül, mert a félévek között 1-1 nap különbség lehet. (Idén például az első félév 182, a második 184 napos volt, a szökőév miatt ez 366 nap.)
Egy év után csakis kamatos kamattal

De mi történik akkor, ha a vásárlás és a lejárat (vagy eladás, visszaváltás) között több mint egy év telik el? Egy év után a konvenciók szerint bizony már kamatos kamatot kell számolni. Így ha például két évre kapunk 20 százalékos kamatot, az biztosan nem évi 10, hanem kevesebb, de mennyi?
Van, ami jó zsebszámológéppel könnyen megy
Ha egy év után valamire kapunk 10 százalék kamatot, majd ezt tovább kamatoztatjuk, akkor a kamat is kamatozik tovább. Az eredmény 1,1*1,1=1,21 lesz, két év után tehát már 21 százaléknál tartunk 20 helyett a kamatos kamat miatt. Az 1,21-ből a tíz százalékot, az 1,1-et gyökvonással kapjuk: 1,21 négyzetgyöke ugyanis 1,1. (A komolyabb zsebszámológépeken van xy vagy yx hatvány – lásd képünket - , a számítógépek kora előtt a kötvénybefektetők varázsszere. A négyzetgyök – második gyök – egyenértékű a 0,5-ik hatvánnyal.)

|
Mit számít egy hétvége? Egy gyakorlati példát az állampapírok köréből kölcsönözhetünk. A július 23. és július 27. között jegyezhető, elsősorban a lakosságnak szánt Kamatozó Kincstárjegy kereken nyolc százalékos kamatot fizet. Egységesített értékpapír hozam mutatója (EHM) viszont csak évi 7,91 százalék. A jelenség magyarázata az, hogy a papír futamideje pár nappal hosszabb, mint egy év, mert a jegyzési idő vége és a kamatozás kezdete között eltelik egy hétvége. Az EHM napra pontosan számol, és ezt is figyelembe veszi. |
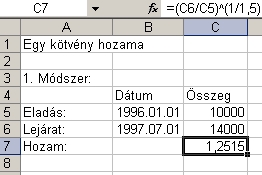
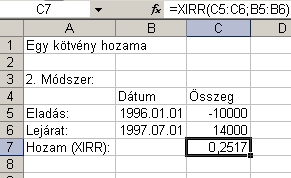
Előző cikkünk példájánál maradva, ha 40 százalékos hozamot kapunk másfél évre, akkor 25,2 százalékos lesz az éves hozamunk. A számítást gyorsan elvégezhetjük zsebszámológéppel is, ennek képlete látható az első módszer nevű képen (lásd lejjebb). A második, könnyebb út az erre szolgáló XIRR nevű Excel-függvény használata. (A két eredmény közötti kis különbséget megint a félévek napjainak száma közötti eltérés okozza.) Ha nem pont évekről, félévekről van szó, akkor sem változik a számítás módszere, csak más számok kerülnek a hatványkitevőbe. Egy 700 napos befektetés kamatos kamattal történő hozamszámításánál például a hatványkitevő értéke 365/700 lesz.
A számítógép melegen ajánlott
Megmarad még az a kérdés, hogyan számolnak kötvényhozamot az egészen bonyolult esetekben, ha nem csak egy kifizetés van hátra, hanem több, nem kerek időszakok vannak hátra, és lehetőleg az eladási ár sem egyezik meg a névértékkel. Az XIRR függvény ebben az esetben is segít, bármely kötvény hozamát könnyedén kiszámolhatjuk vele. A profik zsebszámológéppel is meg tudják oldani a dolgot, ha nem is akkora pontossággal, és főleg sokkal, de sokkal lassabban, mint a számítógép. De hogyan?
Ami még a matematikusoknak sem igen megy
Egy kötvénynél, amelyiknek ismerjük a jövőbeli kifizetéseket és a tőle elvárt hozamot, viszont könnyen meg tudjuk határozni a jelenlegi reális árfolyamát (nettó jelenértékét). Csak el kell osztani mindegyik pénzáramlást a hozamszám (kamatláb) időarányos értékével, és össze kell adni az értékeket. Tulajdonképpen minden törlesztés és kamatfizetés jelenlegi értékét, árfolyamát külön-külön kiszámolják. (Valahogy így számolnak a hitelek törlesztő részleteinél is.)
Hozam helyett számoljunk árfolyamot
Ennek az árfolyamszámításnak a segítségével számolják az ilyen kötvények hozamát is. Meglehetősen egyszerű, de hatékony a módszer: lényegében ki kell totózni, próbálgatni kell. Először megbecsülnek egy várható értéket a hozamra, a rutinos kötvénybefektetőknek általában mindig van némi sejtésük. Azután ezzel a kamatlábbal meghatározzák a kötvény jelenlegi árfolyamát (meghatározzák a pénzáramlások jelenértékét). Ha túl nagy az eltérés, akkor finomítanak egy kicsit a becsült kamatlábon, és kezdik elölről a számítást.
Ezt addig csinálják, amíg megfelelő pontosságú eredményt nem kapnak, a legtöbb gyakorlati esetben nincsen szükség túl nagy precizitásra, féltucatnyi-tucatnyi próbálkozás bőven elegendő lehet. (Ez persze ettől még számológéppel és sok hátralevő kifizetéses kötvénnyel eléggé szörnyű munka lehetett régen.) Ugyanilyen közelítéses (iterációs) módszerrel dolgozik a számítógép is, csak ma már sok milliószor, milliárdszor gyorsabban – a forgalomban levő kötvényeknél a másodperc tört része alatt kidobja az eredményt tucatnyi tizedes jegyig.
(Kizárólag nagyon haladó matekosoknak ajánljuk az ÁKK pénzügyi számításokkal kapcsolatos állásfoglalását.)
Sorozatunk korábbi részei:
Van államadósság, amelyik hasznos, és van, amelyik nem
Ezért jobb az állampapír, mint az akciós betét
Ilyen fajta állampapírok közül tudunk választani
Már Zsigmond király is… a magyar államadósság rövid története
Hozam vagy kamat - így számolj utána a megtévesztő befektetési ajánlatoknak












 Műholdak és űripar.
Műholdak és űripar.













